
카시니의 난형선(Cassini Oval; Cassinisches Oval; 카시니셰스 타원형; 카시니의 타원형...)이라 불리는 곡선은 17세기 천문학자 카시니(Giovanni Domenico Cassini; 1625-1712)에 의해 연구되었던 곡선이다. 카시니는 토성의 위성 중 4개를 발견한 공이 있으며, 토성의 띠에 대한 연구도 활발히 하여 '카시니 사단(Cassini Division)'이라는 부분이 있을 정도다. 심지어 유럽-미국이 운영하는 토성 탐사선의 이름도 '카시니-하위헌스(Cassini-Huygens)'다.
카시니는 'Eléments d'astronomie(천문학 기초, 1740)'라는 책에서 지구에서 바라본 태양의 궤도가 이 곡선일 것이라고 주장했으나, 나중에 뉴턴에 의해 궤도가 타원이라는 것이 증명되며 카시니 난형선은 천문학적 가치를 잃어버리게 된다. 천문학적으로의 가치를 잃기는 했으나, 이 곡선은 동일하게 대전된 전기장의 등포텐셜을 나타내는 곡선으로 물리를 공부하다보면 만날 수 있다.
정의
Cassini Oval은 두 정점 $\mathrm A$, $\mathrm B$에 대해 $\overline {\mathrm {AP}} \times \overline { \mathrm{BP}} = b^2$($b$는 상수)을 만족시키는 점 $\mathrm P$의 자취이다. 타원이 두 정점에서 거리의 합이 일정한 점들로 이루어졌는데 반해, 이 곡선은 거리의 곱이 일정하다. 타원과 카시니 난형선이 각각 두 점까지 거리의 산술평균, 기하평균이 일정한 점이라는 것에 착안해 조화평균이 일정한 곡선도 정의되어 있는데, 그 곡선은 케일리의 타원이라 한다.
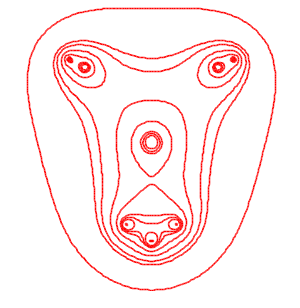
카시니 난형선을 정의할 때 사용된 두 정점을 초점이라고 하는데, 두 초점을 각각 $(a, 0)$, $(-a,0)$이라 하면 카시니 난형선의 방정식은 다음과 같다: $$ \left( (x-a)^2 + y^2 \right) \left( (x+a)^2 +y^2 \right) = b^4$$ 위 식을 다음과 같이 고쳐쓰기도 한다: $$ \left( x^2 +y^2 \right)^2 -2a^2 \left( x^2 -y^2 \right) +a^4 =b^4$$ 이 문서 위에 그려진 그림은 이 곡선의 그래프를 그린 것이다. $a=b$일 때는 무한대 기호 모양의 곡선, lemniscate of Bernoulli가 그려지며, $a \gt b$인 경우에는 분리된 두 달걀모양의 곡선이 그려지고, $a \lt b$인 경우에는 가운데가 패여있는 타원 모양의 곡선이 그려진다.
일반화
고정점의 개수를 늘리거나, $$ \overline{\mathrm{PA_1}} \times \overline{\mathrm{PA_2}} \times \cdots \times \overline{\mathrm{PA}_n} = b^n$$

각각의 길이에 다른 weight를 줘서, $$ \overline{\mathrm{PA_1}}^{w_1} \times \overline{\mathrm{PA_2}}^{w_2} \times \cdots \times \overline{\mathrm{PA}_n}^{w_n} = b^{w_1 + w_2 + \cdots + w_n}$$ 다양한 형태의 변이를 만들 수 있다.
Reference:
Ovale de Cassini
Extrait des Eléments d'astronomie de Jean Cassini (1740) : Depuis l'observation exacte de la grandeur apparente des diamètres du soleil, mon père a trouvé une autre courbe différente de l'ellipse, qui sert à représenter fort exactement les mouvement
mathcurve.com
Cassini oval - Wikipedia
From Wikipedia, the free encyclopedia Class of quartic plane curves Three Cassini ovals, differing by the range within which the parameter e (equal to b/a) falls: 0 < e < 1 e = 1 1 < e < √2 Not shown: e ≥ √2 (convex). In geometry, a Cassi
en.wikipedia.org
Éléments d'astronomie
서평을 찾을 수 없습니다.
books.google.co.kr