수학의 적분공식 중에서 그린의 정리는 정말 강력해 보이는 정리 중 하나다. 그린의 정리는 여러 형태로 표현되지만 여기서는 다음과 같이 표현된 버전을 가지고 이야기를 하려고 한다. $$\oint_C \mathbf F \cdot \mathrm d \mathbf s = \iint_D \left( \frac {\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y}\right) \mathrm d A$$ 위 식에서 $\mathbf F=(F_1, F_2)$는 평면에서 정의된 벡터필드(벡터함수)이며, $C$는 평면의 단일폐곡선, $\mathbf s$는 곡선을 표현하는 벡터함수, $D$는 $C$와 그 내부를 말한다.
위 식을 찬찬히 뜯어보면 좌변은 어떤 도형($D$)의 테두리만을 적분한 값인데, 이 값과 도형 전체에서 계산된 어떤 식의 적분값(우변)이 항상 같아진다는 것을 말한다. 이 정리는 1828년 영국의 수리물리학자 George Green이(1793-1841) An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism이라는 개인소장목적으로 발간된 에세이에서 비슷한 형태의 등식을 소개했고, 이후 코시가 위 등식과 동일한 식을 증명없이 소개했으며, 후에 1851년 리만이 증명했다.
이 글에서는 그린의 정리가 성립하는 이유를 직관적으로 설명하고(절대 증명이 아니다.), 신발끈 공식이 그린의 정리와 어떻게 관계가 있는지를 알아보며, 신발끈 정리를 사용해서 매개변수화 된 단일폐곡선에서 사용할 수 있는 적분공식을 소개한다. 오늘은 저사양 컴퓨터로 작업해서 그림을 그래픽 툴을 이용해서 그리지 못했다. 그래서 그림들이 하나같이 조잡하다. (몇주째 인텔 아톰... ㅠㅠ 텍스트 입력도 버겁다.) 이해해 줬으면 한다.
1. 그린의 정리의 직관적 설명
여기서 설명하는 방식을 싫어하는 사람들도 있겠지만, 그런 분들은 이미 인터넷에 아름다운 증명들이 있기 때문에 그 증명을 참고하면 되겠다. 대표적인 글이라면 아래 위키 사이트가 되겠다.
https://en.wikipedia.org/wiki/Shoelace_formula 이제, 평면 위에 정의된 벡터필드 $\mathbf F$가 있다고 하자.

우리는 이 벡터필드 안에서 다음 곡선을 따라 $\mathbf F \cdot \mathrm d \mathbf s$를 계산할 것이다.
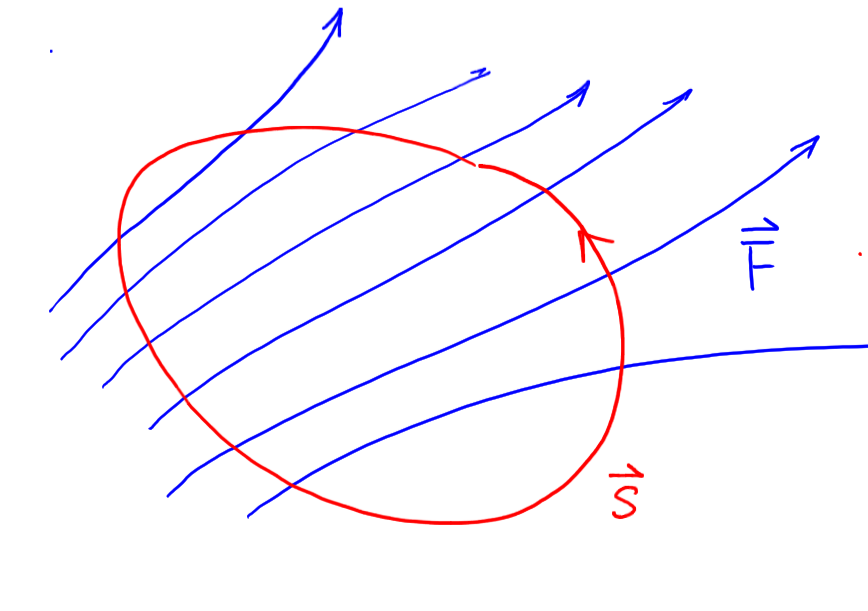
그런데 우리가 계산할 곡선은 아래와 같이 작은 곡선으로 분리할 수 있다.

곡선들은 만나는 곳에서 방향이 반대가 되므로 테두리선을 제외한 지역은 계산과정에서 없어지게 되므로 적분값을 작은 곡선 안에서 먼저 계산하고 더해도 결과는 같다. 이제, 계산의 편의상 이 작은 곡선을 직사각형 모양으로 잡기로 한다. 곡선을 집어넣기 전에 적분 계산을 수행할 지역의 $\mathbf F = (F_1, F_2)$ 값을 다음과 같이 표시한다.

이제, 계산할 때 사용할 곡선을 다음과 같이 그려넣자.

이제, 화살표 방향을 따라서 계산해 나가면 된다. 내적 $\mathbf F \cdot \mathrm d \mathbf s$를 번호를 따라 각각 계산하면 다음과 같다.
1번: $$\mathbf F \cdot \mathrm d \mathbf s = \left\{ (C,D) + t \left( \frac {\partial F_1}{\partial x} \mathrm dx, \frac {\partial F_2}{\partial x} \mathrm dx \right) \right\} \cdot (\mathrm d x, 0) = C \mathrm dx$$ 위 계산과 비슷한 방식으로 다른 부분도 계산하면
2번: $$\left( D + \frac{\partial F_2}{\partial x} \mathrm dx \right) \mathrm dy$$ 3번: $$ - \left( C + \frac{\partial F_1}{\partial y} \mathrm dy \right) \mathrm dx$$ 4번: $$ - D \mathrm d y$$ 이렇게 계산한 결과를 모두 더하면 $$\mathbf F \cdot \mathrm d \mathbf s = \left( \frac{\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y} \right) \mathrm dx \mathrm dy$$ $\mathrm dx \mathrm dy = \mathrm dA$이므로 $$\oint_C \mathbf F \cdot \mathrm d \mathbf s = \iint_D \left( \frac {\partial F_2}{\partial x} - \frac{\partial F_1}{\partial y}\right) \mathrm d A$$
2. 신발끈 공식(Shoelace Formula
신발끈 공식은 1769년 Meister에 의해 발견됐고, 가우스도 1795년에 독립적으로 발견했다. 이 공식은 단순다각형의 이웃한 꼭짓점과 원점을 이용해서 외적을 구한 값(외적의 크기는 삼각형 넓이의 두 배다)을 조합해서 만들어진 것인데, 삼각형 $\mathrm {OAB}$의 넓이를 세 점 $\mathrm O(0,0)$, $\mathrm A(p,q)$, $\mathrm B(r,s)$가 반시계 방향으로 읽힐때는 양의 값으로, 시계방향일 때는 음의 값으로 그 절댓값을 계산해서 더한다. 그런데, 이 결과는 다음 식과 같아진다. $$ \frac 1 2 (ps-rq) = \frac 1 2 \det \left( \begin{matrix} p &r \\ q & s \end{matrix} \right) := \frac 1 2 \det(\mathrm A, \mathrm B)$$ 위에서 점의 좌표는 통상적인 약속에 맞게 하기 위해 $\mathrm A$, $\mathrm B$ 순으로 세로로 배열했다.

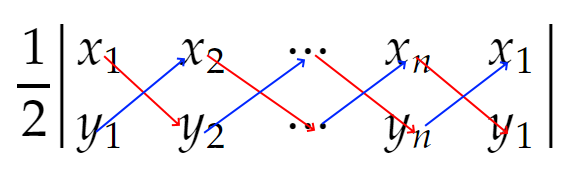
위와 같은 다각형의 경우 $\det( \mathrm A, \mathrm B)$, $\det(\mathrm B, \mathrm C)$, $\det(\mathrm C, \mathrm D)$, $\det(\mathrm D, \mathrm E)$, $\det (\mathrm E, \mathrm A)$를 차례로 구하면 $\det(\mathrm C, \mathrm D)$, $\det(\mathrm E, \mathrm A)$가 음수고 나머지가 모두 양수가 되므로 이 수들의 총합이 다각형의 넓이와 같음을 알 수 있다. 방향을 신경쓰지 않아도 되도록 꼭짓점이 $(x_i, y_i)$ ($i=1,2, ...,n$)인 단순다각형의 넓이를 구하는 신발끈 공식은 다음과 같은 모양을 하고 있다. (단, $x_{n+1} = x_1$, $y_{n+1} = y_1$) $$ \frac 1 2 \left| \begin{matrix} x_1 & x_2 & \cdots &x_n & x_1 \\ y_1 & y_2 & \cdots & y_n & y_1 \end{matrix} \right| = \frac 1 2 \left| \sum_{i=1}^n \det \left( \begin{matrix} x_i & x_{i+1} \\ y_i & y_{i+1} \end{matrix} \right) \right|$$
이 계산방식이 아래와 같이 신발끈 형태라고 해서 신발끈 공식이라고 한다. (빨간 색은 $+$, 파안 색은 $-$로 계산)
이 신발끈 공식을 그린 정리를 이용해서 계산해 보자. $\mathrm O(0,0)$, $\mathrm A(a,b)$, $\mathrm B(c,d)$를 세 꼭짓점으로 하는 삼각형의 세 변을 아래 그림과 같이 계산순서를 잡고 각각 $0 \leq t \leq 1$을 변수로 해서 각각 곡선의 방정식을 만든다.

삼각형 $\mathrm {OAB}$의 넓이는 적분 $$ \iint_{\mathrm{OAB}} \mathrm dA$$ 로 계산되므로 $\mathbf F = (y,2x)$라 하고 위 곡선을 따라 선적분을 하면 넓이가 얻어짐을 알 수 있다. 실제 계산을 하면
경로 [1]: $$\int_0^1 (bt,2at) \cdot (a,b) \mathrm dt = \int_0^1 3abt \mathrm dt = \frac 3 2 ab$$ 경로 [2]: $$\int_0^1 ((d-b)t +b , 2(c-a)t+2a) \cdot (c-a,d-b) \mathrm dt = \frac 3 2 (c-a)(d-b) +b(c-a)+2a(d-b)$$ 경로 [3]: $$\int_1^0 (dt,2ct) \cdot (c,d) \mathrm dt = - \frac 3 2 dc$$ 이렇게 구한 결과를 다 더하면 다음과 같은 결과를 얻는다. $$\iint_{\mathrm {OAB}} \mathrm dA = \frac 1 2 (ad-bc) = \det(\mathrm A, \mathrm B)$$
3. 매개화된 단순곡선 내부의 넓이를 구하는 공식
앞서 구한 신발끈 공식을 이용해서 단순폐곡선 $\mathrm s(t)$($t_i \leq t \leq t_f$)의 내부의 넓이를 구하는 식을 얻어낼 수 있다. 평면위의 임의의 단순폐곡선은 다음과 같이 삼각형 모양의 도형을 더한 것으로 볼 수 있다.

그러면 정적분의 정의와 신발끈의 공식을 이용해서 이 곡선의 내부 넓이는 다음과 같이 계산할 수 있음을 알 수 있다. $$\frac 1 2 \left| \int_{t_i}^{t_f} \det( \mathbf s(t), \mathbf s(t+dt) ) \mathrm dt \right| = \frac 1 2 \left| \int_{t_i}^{t_f} (x(t) y'(t) - y(t) x'(t)) \mathrm dt \right|$$