이 글은 3차원 (비퇴화) 곡선의 분석을 위해 사용되는 프레네-세레 공식(Frenet-Serret Formula)에 대해 다룬다. 편의상 이 글에서 다루는 곡선은 이 글의 범위에서 사용하는 수식에 문제를 일으키지 않을 만큼 평범한 부드러운 곡선이라고 가정하자.
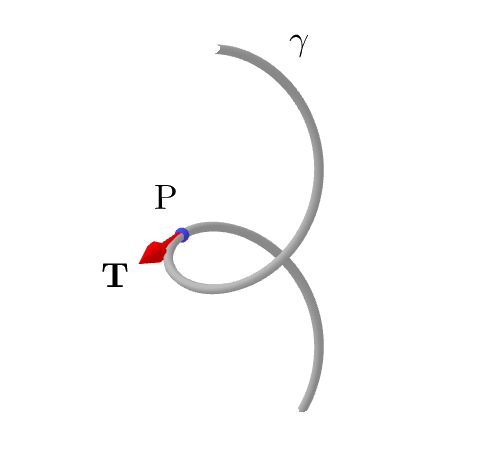
아래 그림은 곡선 $\gamma(t)$와 그 위의 점 $\mathrm P = \gamma(t_0)$를 표현한 것이다. 점 $\mathrm P$는 편의상 아래에서 위로 올라온다고 가정한다.

이제, 이 그림에 접선벡터 $\mathbf T = \gamma'(t_0)$를 표시하면 다음과 같다.
임의의 실수 $t$에 대해 $\gamma'(t)$를 알고있다면 당연히 $\gamma(t)$를 얻어낼 수 있겠지만 여기서 하려는 것은 곡선의 방정식을 구하는 것이 아니라 공간을 지나는 곡선을 기하학적으로 묘사하는 방법에 대한 것이다. 이것을 위해 곡선의 변수 $t$를 적당히 조절해서 (대체로 곡선의 길이를 가지고 처리한다. 대부분의 책에 이렇게 정의한 변수를 $s$로 새로 정의하지만, 이 글에서는 그냥 $t$를 사용하겠다.) $\mathbf T$의 크기가 항상 $1$이 되도록 설정되어 있다고 하자. 그러면 $\mathbf T \cdot \mathbf T =1$에서 $$ \mathbf T' \cdot \mathbf T =0$$ 이 얻어진다. 즉, $\mathbf T'$은 벡터 $\mathbf T$에 항상 수직이다. 다시 말해 $\mathbf T'$은 아래 그림에 표시된 평면($\mathbf T'$에 수직인 평면) 어딘가에 포함된다.
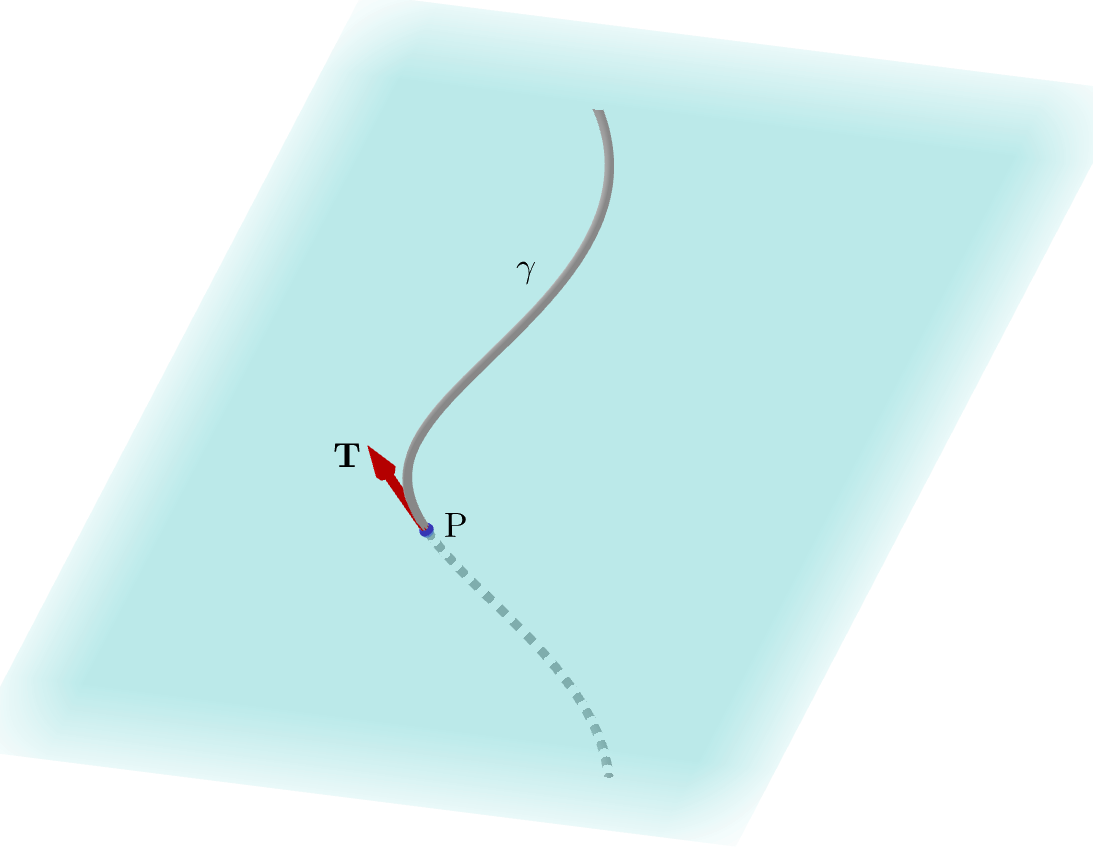
평면곡선에서 곡선의 위치벡터 $\gamma(t)$를 두 번 미분한 것을 가지고 곡률을 계산했던 경험을 여기로 가져와서 공간에서도 $\mathbf T'$으로 곡선의 휘어진 정도를 나타내는 것은 합리적으로 보인다. 이 벡터와 같은 방향의 단위벡터를 법선벡터(normal vector) $\mathbf N$이라 하면 벡터 $\mathbf N$은 아래 그림과 같이 먼저 언급한 평면에 포함되는 단위벡터가 된다.

기존의 경험에 따르면 두 단위벡터 $\mathbf T$와 $\mathbf N$으로 평면 안에 포함된 곡선을 곡률을 사용해 묘사할 수 있었다. 그때문에 지금 다루는 3차원 공간에 놓여진 곡선의 해석은 기존의 두 벡터(접선벡터, 법선벡터)로는 정확히 묘사할 수 없다는 것을 쉽게 예상할 수 있다. 실제로, $\mathrm P$에서 위 그림과 동일한 $\mathbf T$, $\mathbf N$을 가지더라도 위 그림처럼 우리가 보는 곳에서 멀어지는 방향으로 비틀린 곡선이 있을 수도 있지만 가까운 방향으로 비틀린 곡선도 가능하다. 이런 변화를 설명할 수 있으려면 추가 벡터가 필요한데, 그간 우리가 잡던 공간좌표계의 관행상 오른손 법칙을 적용해서 $\mathbf T \times \mathbf N$을 나머지 한 벡터로 잡는 것이 자연스럽다. 이 벡터를 이중법선벡터(binormal vector)라 하고 $\mathbf B$로 쓴다.

이렇게 세 벡터를 정의했다. 이렇게 정의하면 $\mathbf T \times \mathbf N = \mathbf B$, $\mathbf N \times \mathbf B = \mathbf T$, $\mathbf B \times \mathbf T = \mathbf N$이 성립한다. Frenet-Serret Formula는 이 세 벡터들과 그 미분 사이의 관계식이다.
$\mathbf T'$에 대해
우선, $\mathbf T'$의 크기를 $\kappa$라 하면 $\mathbf N$의 정의에 의해 \begin{equation} \label{eq0} \mathbf T' = \kappa \mathbf N \end{equation} 이 성립한다. $\kappa$를 “곡률(curvautre)”이라 한다.
$\mathbf B'$에 대해
$\mathbf B$는 미분을 이용하지 않고 정의되어 있는데, 이 정의는 특이한 결과를 유도해낸다. $\mathbf B$를 미분해 보면, \begin{equation} \label{eq1} \mathbf B ' = ( \mathbf T \times \mathbf N)' = \mathbf T' \times \mathbf N + \mathbf T \times \mathbf N' = \mathbf T \times \mathbf N' \end{equation} 으로, $\mathbf B'$이 $\mathbf T$에 항상 수직임을 알 수 있다.
위 결과식의 의미를 한 번 짚고 넘어가자. 점 $\mathrm P$가 움직이는 방향을 $\mathbf T$가 가리키므로 $\mathrm P$의 위치가 변함에 따라 $\mathbf T$도 바뀌고 그 결과로 $\mathbf T$에 수직인 평면도 시시각각 변한다. 그러면 자연스럽게 $\mathbf B$, $\mathbf N$도 변하는데, $\mathbf B$뿐 아니라 $\mathbf B$가 변하는 방향도 $\mathbf T$에 수직이 된다는 것을 의미한다. 이 현상은 $\mathrm T$의 미분을 벡터 $\mathbf N$의 정의에 포함시켰기 때문에 생기는 것이다.
$\mathbf B$가 크기가 일정한 벡터이므로 $\mathbf B'$은 $\mathbf B$에도 수직이다. 따라서, $\mathbf B'$은 $\mathbf N$에 평행이다. 즉, \begin{equation} \label{eq2} \mathbf B' = - \tau \mathbf N \end{equation} 이라고 쓸 수 있다. $\tau$를 “곡선비틀림(torsion)”이라 한다.
$\mathbf N'$에 대해
우선, 벡터 $\mathbf N$도 크기가 일정한 벡터이므로 $\mathbf N'$은 $\mathbf N$에 수직이다. 따라서, \begin{equation} \label{eq3} \mathbf N' = \alpha \mathbf T + \beta \mathbf B \end{equation} 라고 놓을 수 있다.
이제, 식 (\ref{eq2})과 (\ref{eq3})를 (\ref{eq1})에 대입하면 \begin{align*} - \tau \mathbf N &= \mathbf T \times ( \alpha \mathbf T + \beta \mathbf B) \\ &= \beta \mathbf T \times \mathbf B \\ &= - \beta \mathbf N \end{align*} 따라서, $\beta = \tau$이다. 마찬가지로, $\mathbf T = \mathbf N \times \mathbf B$라는 사실과 $\mathbf B'$이 $\mathbf N$과 평행이라는 사실을 이용하면 \begin{equation} \label{eq4} \mathbf T' = ( \mathbf N \times \mathbf B)' = \mathbf N' \times \mathbf B + \mathbf N \times \mathbf B' = \mathbf N' \times \mathbf B \end{equation} 이 얻어진다. 이 식에 식 (\ref{eq0}), (\ref{eq3})을 대입하면 \begin{align*} \kappa \mathbf N &= (\alpha \mathbf T + \beta \mathbf B) \times \mathbf B \\ &= \alpha \mathbf T \times \mathbf B \\ &= - \alpha \mathbf N \end{align*} 이 되므로 $\alpha = - \kappa$가 된다. 즉, \begin{equation} \label{eq5} \mathbf N ' = - \kappa \mathbf T + \tau \mathbf B \end{equation}
식 (\ref{eq5})은 직관적 해석도 가능하다.
식 (\ref{eq3})을 만들면서도 생각을 했지만 $\mathbf N'$은 $\mathbf N$과 수직이다. 그래서 $\mathbf N$은 $\mathbf T$, $\mathbf B$의 방향으로만 변형이 이루어짐을 알 수 있다. $\mathbf N'$을 $\mathbf T$, $\mathbf N$, $\mathbf B$를 basis로 가지는 3차원 공간에서 정의된 일차변환의 결과값이라 생각하면 우리는 $\mathbf N'$은 $\mathbf N$을 공간상에서 확대, 축소, 회전을 조합해 얻어낸 벡터로 볼 수 있다. 그리고, 그 결과는 세 벡터의 방향을 회전축으로 각각 얻어낸 결과를 서로 더해도 된다. 이제, 벡터 $\mathbf T$ 방향을 회전축으로 보았을 때 $\mathbf N$이 어떻게 변하는지 살펴보자. 그러면 벡터 $\mathbf N$의 변화는 아래 그림과 같이 $\mathbf N$-$\mathbf B$평면 안에서 이루어지는 것처럼 보일 것이다.

그런데, 식 (\ref{eq2})에서 $\mathbf B' = -\tau \mathbf N$이므로 $\mathbf B$는 아래 그림과 같이 변하고 있다.

그러면 $\mathbf B$와 수직 관계를 유지해야 하는 $\mathbf N$은 아래와 같이 변해야 한다.

따라서, $\mathbf N'$은 $\tau \mathbf B$를 포함해야 한다. 이제 $\mathbf B$ 방향을 회전축으로 해서 같은 논리를 적용하면 $- \kappa \mathbf T$를 포함해야 함을 알 수 있다. 따라서, $\mathbf N' = -\kappa \mathbf T + \tau \mathbf B$이다.