이 글은 적분식에 나타나는 $\mathrm dx$가 무엇인지에 대한 설명을 담고 있다. 대상독자를 학부 저학년 수준으로 잡아보았는데, 원래 정의를 많이 손상시키지 않으면서 설명해 보려고 했다. 다차원에서는 복잡한 이야기를 추가해야 하기 때문에 여기서는 1변수에 한정해서 설명한다.
1. 역사적 배경
라이프니츠가 처음 미분기호 $\dfrac {\mathrm dy}{\mathrm dx}$를 고안해 냈을 때, 이 기호는 분수의 뜻을 가졌다. $\mathrm dy$와 $\mathrm dx$는 독립적으로 쓰일 수도 있었고 해당 기호는 각각 $y$, $x$의 미세한 변화량을 의미했다. 라이프니츠에 의하면 ‘미세한 양’이라는 것은 너무 작아서 아무리 더해도 1보다 작은 값을 가지는 양수였었다. 하지만, 이런 양수는 Archimedean Property를 만족하지 않는다. 즉, 미적분학에서 사용하게 되는 실수의 집합에는 $\mathrm dx$에 해당하는 수가 없었다. 라이프니츠의 미분 정의는 후에 평균변화율의 극한으로 바뀌면서 $\dfrac {\mathrm dy}{\mathrm dx}$은 분수개념이 아닌 $\dfrac {\mathrm d}{\mathrm dx} y$와 같이 함수에 작용하는 연산자 역할로 해석이 되었다.
라이프니츠는 미분보다 적분을 먼저 발견했는데, 이 과정이 $\mathrm dx$가 앞서 말한 개념을 가지게 된 결정적인 원인을 제공했다. 후에 비표준해석학이라는 수학 분야를 만든 수학자들은 라이프니츠의 개념을 갖고 미적분학을 할 수 있는 방법을 제공해 주었다. 하지만, 이것은 현재 사용하는 실수와 좀 다른 수체계에서 해석학을 해야 하므로 수체계가 다소 복잡해진다. 이런 단점에도 불구하고 비표준해석학은 라이프니츠의 방식으로 계산하더라도 대부분의 문제에서 큰 탈이 생기지 않음을 보증해 주었다.
라이프니츠의 오개념에서 만들어진 적분기호는 계산의 편의성 덕에 지금도 사용되고 있다.
2. 세 가지 $\mathrm dx$
대학과정 전에 배우는 미적분학에서는 $\mathrm dx$에 큰 의미를 부여하지 않는다. 학부과정에서 이 기호의 뜻을 배우게 되는데, 이 기호의 개념은 하나가 아니다. 그 개념은 크게 세 가지로 나눌 수 있는데, 부정적분, 측도(measure), 미분형식(differential form)의 세 분야에서 다루는 개념으로 나눠서 설명할 수 있겠다. 이 내용에 대해서는 테렌스 타오가 Differential Forms and Integration이라는 에세이에서 잘 다루어 놓았다. 다차원에 대한 설명도 들어있으므로 참고하기 바란다. 이 글도 타오의 에세이를 참고해서 작성되었다.
2.1. 부정적분, $\displaystyle{\int f(x) \mathrm dx}$
이 경우의 $\mathrm dx$는 중앙에 있는 수식 $f(x)$의 $x$에 대한 원시함수 $F(x)$, 즉, $\dfrac {\mathrm d}{\mathrm dx}F(x) = f(x)$를 만족하는 함수를 얻어내기 위한 계산을 표시하는 기호의 오른쪽 괄호(수식의 끝 표시) 역할을 한다. (왼쪽 괄호는 적분기호 $\displaystyle{\int}$이다.) 정적분의 치환적분과 같은 치환적분이 가능하지만, 이것은 미분방정식 $\dfrac {\mathrm d}{\mathrm dx}F(x) = f(x)$이 치환에 의해 변형되기 때문에 생기는 현상이다.
2.2. 측도적분, $\displaystyle{\int_{[a,b]} f(x) \mathrm dx}$
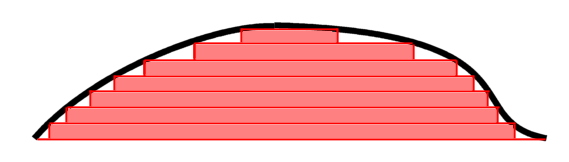
측도 적분의 경우에는 $\mathrm dx$보다는 계산에 사용할 측도(길이/크기를 재는 규칙으로 생각하면 된다.)를 사용해서 $\mathrm d \mu(x)$, $\mu(\mathrm dx)$와 같은 형태로 적는다. 이 기호는 계산에 사용할 측도를 표현하는 기능을 한다. 측도적분은 다음 그림과 같이 가로로 쪼개서 계산하므로 계산결과는 0이상의 값이 나오는 것이 일반적이다. 측도가 달라지는 경우에 라돈-니코딤 정리를 활용해서 라돈-니코딤 미분 $\dfrac {\mathrm d \nu} {\mathrm d \mu}$을 구해서 처리할 수 있다. $f$가 일변수함수이고 $a \leq b$일 때 정적분과 다음 관계를 가진다. $$\int_{[a,b]} f(x) \mathrm dx = \int_a^b f(x) \mathrm dx =- \int_b^a f(x) \mathrm dx$$
2.3. 정적분, $\displaystyle{\int_a^b f(x) \mathrm dx}$
이 적분은 라이프니츠의 적분개념을 계승한 적분이다. 이 식에 쓰이는 $\mathrm dx$는 미분형식(differential form)이라는 함수다. 좀 더 구체적으로 말한다면 함수 $\mathrm d x: T_x \to \mathbb R$는 $x$를 시점으로 하는 벡터공간 $T_x$에서 실수로 가는 함수로, $$\mathrm d x( k \mathbf e_x) = k \quad (k \in \mathbb R)$$ 이다. 마찬가지로, 적분 안의 식 $f(x) \mathrm d x$도 $T_x$에서 정의된 함수이다. 고등학교 적분 정의에 따르면 $a$를 시점으로 하는 벡터 $3 \mathbf e_x$는 $3f(a)$라는 함숫값을 갖는다. 이 함수에 적분기호 $\displaystyle{\int_a^b}$가 적용되면 제한된 조건하에 계산된 함수값 $f(x) \mathrm d x( \cdot)$의 극한을 계산하는 것이 되고, 그 계산법에 따라 여러 가지 적분 이름이 붙는다. 고등학교 교과과정에 나온 정의식 $$\int_a^b f(x) \mathrm dx = \lim_{n \to \infty} \sum_{k=1}^n f \left( a + (b-a) \frac k n\right) \frac {b-a} n$$ 에서는 $f(x) \mathrm d x( \cdot)$의 값을 $x = a+\dfrac {(b-a)k} n$($k=1,2, \cdots, n$)에서 벡터 $\dfrac{b-a}n \mathbf e_x$를 계산한 후 더했다. 적분은 이 값들의 극한값이다. 도함수가 연속인 함수 $f$에 대해 미분형식 $\mathrm df$는 다음 식을 만족하는 함수다. $$\lim_{h \to 0} \left| \frac{f(x+h)-f(x)}{h} - \mathrm df\right| = 0$$ 따라서, $\mathrm df = f'(x) \mathrm dx$라는 식을 얻을 수 있다.
3. 표기의 문제
수학책이나 논문에서 보이는 $\mathrm dx$의 표기는 두 가지가 있다. 하나는 이 문서에서처럼 d를 세워서 쓰는 방식이고, 다른 하나는 단순히 $dx$라고 쓰는 방식이다. 수식을 입력하는 입장에서는 후자가 편하기는 하지만, 예약된 기호나 함수 이름, 점의 이름은 세로로 쓰는 관례에 따라 d만 따로 로만체로 쓰는 사람들도 있다.
4. 참고자료
- Terrence Tao, Differential Forms and Integration
학부생들이 참고하면 좋은 글이다. 다차원에 대한 설명까지 들어있다. - Elliott H. Lieb and Michael Loss, Analysis, 2nd Edition, Graduate Studies in Mathematics, Vol. 14, American Mathematical Society, 2000.
첫단원부터 적분으로 시작하는 실해석학책. 측도론과 적분을 잘 연결해 놓았다. - Harold M. Edwards, Advanced Calculus: A Differential Forms Approach, Modern Birkhäuser Classics, Birkh&amul;user, 2014
differential form에서 시작하는 고등미적분학. differential form을 비롯한 여러 계산에 대한 가이드가 잘 되어 있다.